【データ分析】住宅価格データを使って線形回帰モデルの精度の向上に挑戦してみる

こんにちは、爽です。皆さん、いかがお過ごしでしょうか?
今回は以前に構築した線形回帰モデルの精度向上に挑戦してみたいと思います。
以前、scikit-learnのボストンの住宅価格データを使って、モデルを構築してモデルの可視化まで行ってみましたが、今回はさらに一歩踏み込んだ内容となります。
なお、今回の記事の目的は目的変数を完全に予測できるモデルを構築することではなく、モデルの精度向上する際の観点をまとめて実践までしてみることです。従って、Kaggleとかでスコアを上げたいと考えている人には向いていない記事だと思います。(そもそもKaggleに取り組んでる人はこの記事は見てないと思いますが。笑)
・【データ分析】scikit-learnを使って住宅価格データを分析・機械学習してみる
■この記事の対象読者
・データ分析に興味のある方
なお、私はPythonをAnacondaをインストールしてJupyterで実行しています。MacのAnacondaのインストール方法とJupyterの使い方は下記記事にまとめているので良かったらご参考ください。
それではどうぞ!
前回記事のおさらい
まずは前回私がどのようなモデルを作成したか、その結果と可視化結果を載せます。
from sklearn.datasets import load_boston
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
boston = load_boston()
#データフレームに変換
df = pd.DataFrame(boston.data, columns=boston.feature_names)
df['MEDV'] = boston.target
#説明変数
X = df.iloc[:,:-1].values
#目的変数
y = df['MEDV'].values
#訓練データとテストデータの準備
from sklearn.model_selection import train_test_split
#既存のデータをトレーニングデータとテストデータに分割
# パラメータ:test_sizeでテストに使うデータの割合を指定可能
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0)
#linear_modelをimport
import sklearn.linear_model
#予測モデルの初期化
classifier = sklearn.linear_model.LinearRegression()
#Xを入力した時にyを出力するように学習
classifier.fit(X_train, y_train)
#モデル評価
from sklearn.metrics import mean_squared_error
y_prediction = classifier.predict(X_test)
print("平均二乗誤差(トレーニングデータ): ", mean_squared_error(y_train, y_train))
print("平均二乗誤差(テストデータ): ", mean_squared_error(y_test, y_prediction))
#予測結果の格納
y_pred = classifier.predict(X)
#グラフの描画
fig, ax = plt.subplots()
ax.scatter(y, y_pred, edgecolors=(0, 0, 0))
ax.plot([y.min(), y.max()], [y.min(), y.max()], 'k--', lw=4)
ax.set_xlabel('Measureed')
ax.set_ylabel('Predicted')
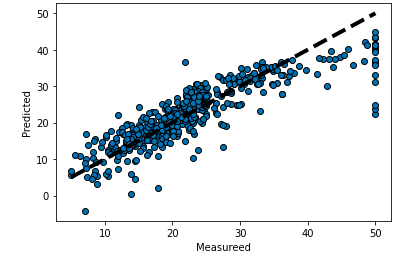
plt.show()
# 平均二乗誤差(トレーニングデータ): 0.0
# 平均二乗誤差(テストデータ): 27.195965766883234前回はデータの前処理は特にせず、変数もとりあえず全部突っ込んでモデルを構築してみました。
また、モデルの評価についてはMSEという評価指標を使ってモデルの評価を行いました。
MSEは「平均二乗誤差(Mean Squared Error: MSE)」といい、モデルの誤差が大きいほど値が大きくなり、逆に誤差が小さいほど値も小さくなる指標です。
今回もこの評価指標を用いて、この数値をより小さくしていくことでモデルの精度向上を目指します。
また、何の処理が精度向上に寄与したかを確認するために、モデル精度の確認は細かく実施していきたいと思います。
データの前処理による精度向上
まず、前回モデルを構築した際はデータの統計量を確認しただけで、データの前処理はしなかったので、今回は実施してみたいと思います。例えば外れ値があるとその外れ値の影響でモデルの精度が落ちることもあります。
まずは統計量を確認。
df.describe()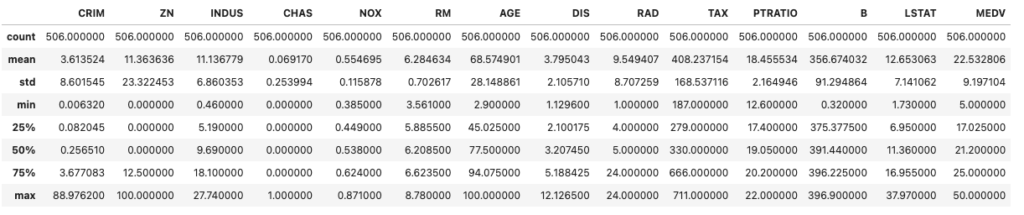
各列の意味も再掲します。
- CRIM: 町別の「犯罪率」
- ZN: 25,000平方フィートを超える区画に分類される住宅地の割合=「広い家の割合」
- INDUS: 町別の「非小売業の割合」
- CHAS: チャールズ川のダミー変数(区画が川に接している場合は1、そうでない場合は0)=「川の隣か」
- NOX: 「NOx濃度(0.1ppm単位)」=一酸化窒素濃度(parts per 10 million単位)。この項目を目的変数とする場合もある
- RM: 1戸当たりの「平均部屋数」
- AGE: 1940年より前に建てられた持ち家の割合=「古い家の割合」
- DIS: 5つあるボストン雇用センターまでの加重距離=「主要施設への距離」
- RAD: 「主要高速道路へのアクセス性」の指数
- TAX: 10,000ドル当たりの「固定資産税率」
- PTRATIO: 町別の「生徒と先生の比率」
- B: 「1000(Bk – 0.63)」の二乗値。Bk=「町ごとの黒人の割合」を指す
- LSTAT: 「低所得者人口の割合」
- MEDV:「住宅価格」(1000ドル単位)の中央値。通常はこの数値が目的変数として使われる
※参考外部リンク:https://atmarkit.itmedia.co.jp/ait/articles/2006/24/news033.html
外れ値除去
まずは外れ値を除去します。
3σ法の概念を用いて、平均より標準偏差が3σ以上のものを弾いていきます。
いわゆる統計学的には平均から±1標準偏差が全体の約68%、±2標準偏差が全体の約95%、±3標準偏差が全体の97.7%をカバーしていることから、それ以降の数字は外れ値として見なすことができるため、それを除去していきます。
ただし、この手法は変数の値が正規分布であることを前提としている為、正規分布ではない変数に適用すると分析がうまくいかないケースもあるので注意が必要です。今回はカテゴリ変数は存在しない為、とりあえず全変数に対して3σ法を適用していきます。
#平均取得
mean = df.mean()
#標準偏差取得
sigma = df.std()
#列名取得
cols = df.columns
_df = df
#ループで外れ値を除去する
for col in cols:
low = mean[col] - 3 * sigma[col]
high = mean[col] + 3 * sigma[col]
_df = _df[(_df[col] > low) & (_df[col] < high)]
#元のデータフレーム
print(len(df))
#外れ値除去後のデータフレーム
print(len(_df))
# 506
# 415外れ値を除去できたか統計量で確認します。
CRIMはmaxが88くらいですが、除去後はmaxが28になっているので、外れ値除去はできていそうなことが分かります。
df.describe()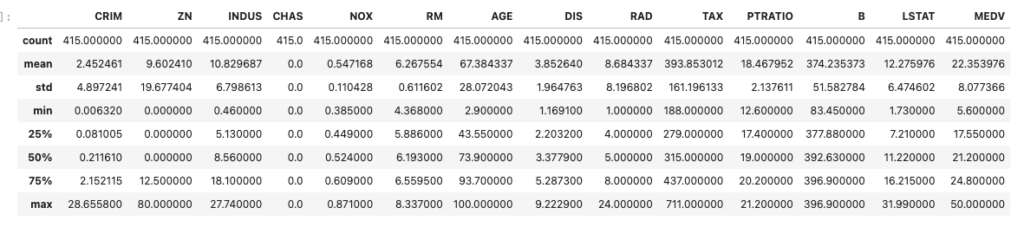
モデルの精度を確認します。
#説明変数
X = _df.iloc[:,:-1].values
#目的変数
y = _df['MEDV'].values
#訓練データとテストデータの準備
from sklearn.model_selection import train_test_split
#既存のデータをトレーニングデータとテストデータに分割
# パラメータ:test_sizeでテストに使うデータの割合を指定可能
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0)
#linear_modelをimport
import sklearn.linear_model
#予測モデルの初期化
classifier = sklearn.linear_model.LinearRegression()
#Xを入力した時にyを出力するように学習
classifier.fit(X_train, y_train)
#モデル評価
from sklearn.metrics import mean_squared_error
y_prediction = classifier.predict(X_test)
print("平均二乗誤差(テストデータ): ", mean_squared_error(y_test, y_prediction))
y_pred = classifier.predict(X)
#グラフの描画
fig, ax = plt.subplots()
ax.scatter(y, y_pred, edgecolors=(0, 0, 0))
ax.plot([y.min(), y.max()], [y.min(), y.max()], 'k--', lw=4)
ax.set_xlabel('Measureed')
ax.set_ylabel('Predicted')
plt.show()
# 平均二乗誤差(テストデータ): 17.083504944427848外れ値を除去しただけで除去せずに学習した時よりもスコアがかなり改善されました!
この結果はデータの前処理にて統計量を確認した上で外れ値を除去することはかなり重要であることを示唆しています。
説明力のある変数の選定
次に学習の際に用いる変数を選定していきます。
学習させても説明力が上がらない変数を含めてモデルを学習させても、精度は良くな流どころか、むしろ下がってしまったり、学習に時間がかかってしまう原因となってしまう為、説明変数の選定も非常に重要だと考えます。今回はstatsmodelsを用いて変数の説明力を確認します。
import statsmodels.api as sm
x1 = _df.iloc[:,:-1]
x = sm.add_constant(x1)
results = sm.OLS(y,x).fit()
results.summary()
# OLS Regression Results
# ==============================================================================
# Dep. Variable: y R-squared: 0.744
# Model: OLS Adj. R-squared: 0.736
# Method: Least Squares F-statistic: 97.37
# Date: Fri, 09 Sep 2022 Prob (F-statistic): 7.59e-111
# Time: 22:50:46 Log-Likelihood: -1172.6
# No. Observations: 415 AIC: 2371.
# Df Residuals: 402 BIC: 2424.
# Df Model: 12
# Covariance Type: nonrobust
# ==============================================================================
# coef std err t P>|t| [0.025 0.975]
# ------------------------------------------------------------------------------
# const 25.9707 5.492 4.729 0.000 15.173 36.768
# CRIM -0.1532 0.075 -2.043 0.042 -0.301 -0.006
# ZN 0.0056 0.015 0.384 0.701 -0.023 0.034
# INDUS 0.0173 0.056 0.308 0.758 -0.093 0.128
# CHAS 3.013e-13 6.44e-14 4.677 0.000 1.75e-13 4.28e-13
# NOX -11.5783 3.913 -2.959 0.003 -19.271 -3.885
# RM 5.0607 0.473 10.709 0.000 4.132 5.990
# AGE -0.0214 0.012 -1.722 0.086 -0.046 0.003
# DIS -1.2203 0.197 -6.189 0.000 -1.608 -0.833
# RAD 0.2508 0.068 3.680 0.000 0.117 0.385
# TAX -0.0119 0.003 -3.456 0.001 -0.019 -0.005
# PTRATIO -0.9156 0.124 -7.407 0.000 -1.159 -0.673
# B 0.0055 0.004 1.277 0.202 -0.003 0.014
# LSTAT -0.4361 0.057 -7.700 0.000 -0.547 -0.325
# ==============================================================================
# Omnibus: 227.699 Durbin-Watson: 1.192
# Prob(Omnibus): 0.000 Jarque-Bera (JB): 2516.429
# Skew: 2.102 Prob(JB): 0.00
# Kurtosis: 14.308 Cond. No. 1.92e+18
# ==============================================================================
ごちゃっとした表が出てきましたが、今回は「P>|t|」が0.05以上の有意ではない変数を分析から外します。
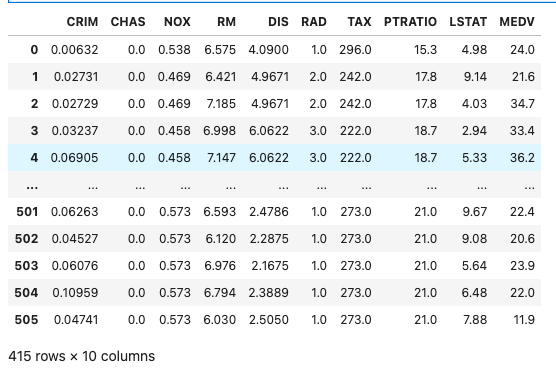
_df = _df.drop(['ZN', 'INDUS', 'AGE', 'B'], axis=1)
_dfこれでもう1回学習させてみます。
#説明変数
X = _df.iloc[:,:-1].values
#目的変数
y = _df['MEDV'].values
#訓練データとテストデータの準備
from sklearn.model_selection import train_test_split
#既存のデータをトレーニングデータとテストデータに分割
# パラメータ:test_sizeでテストに使うデータの割合を指定可能
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0)
#linear_modelをimport
import sklearn.linear_model
#予測モデルの初期化
classifier = sklearn.linear_model.LinearRegression()
#Xを入力した時にyを出力するように学習
classifier.fit(X_train, y_train)
#モデル評価
from sklearn.metrics import mean_squared_error
y_prediction = classifier.predict(X_test)
print("平均二乗誤差(テストデータ): ", mean_squared_error(y_test, y_prediction))
# 平均二乗誤差(テストデータ): 17.05715850125408本当に僅かにモデル精度が改善しましたが、大きな改善には至りませんでした。
しかし、変数を減らしても精度はあまり変わらないということは、精度はそのままで学習にかかるコストが減ったということですので、特に大量データを扱う際は、変数の選定は重要な観点になるかと思います。
モデル自身の精度向上
この記事を書く前は、LinearRegressionのチューニングをGridSerchを使って精度向上しようと思っていたのですが、よくよく調べるとLinearRegressionはチューニングの余地があまりないことが判明しました。従って、他の方法で精度向上を図ってみたいと思います。
モデルの変更
まずはモデルをLinearRegressionから違うモデルに変えてみます。
使うモデルはKagglerがよく用いる勾配ブースティング木モデルのLightGBMです。Udemyでもよくゴリ押しされているモデルなので、今度詳細調べてこのブログでまとめてみたいですが、今回は一旦使ってみて精度向上するにとどめます。
import lightgbm as lgb
# モデルの学習
model = lgb.LGBMRegressor() # モデルのインスタンスの作成
model.fit(X_train, y_train) # モデルの学習
#モデル評価
from sklearn.metrics import mean_squared_error
y_prediction = model.predict(X_test)
print("平均二乗誤差(テストデータ): ", mean_squared_error(y_test, y_prediction))
y_pred = model.predict(X)
#グラフの描画
fig, ax = plt.subplots()
ax.scatter(y, y_pred, edgecolors=(0, 0, 0))
ax.plot([y.min(), y.max()], [y.min(), y.max()], 'k--', lw=4)
ax.set_xlabel('Measureed')
ax.set_ylabel('Predicted')
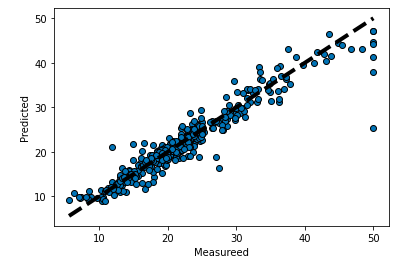
plt.show()
# 平均二乗誤差(テストデータ): 12.427205847610871なんとモデルを変えただけで精度が向上してしまいました。さすがLightGBMです。
本来ならLightGBMでもチューニングを行うべきですが、パラメータの数が多そうなので、ここのチューニングは別の機会にまとめてみたいと思います。
訓練方法の変更
もう一つ、モデルの訓練方法変えることでもモデルの精度向上を目指してみます。
今まではscikit-learnのtrain_test_splitを使ったhold-out法での訓練でしたが、今度は交差検証を使って訓練をしてみます。
hold-out法は訓練データを1度しか学習しないのに対し、交差検証法は訓練データと検証データを使って何度か自分で学習する方法で、この方法だと全ての訓練データを用いて学習ができる為、モデルの精度向上が期待できます。
#説明変数(ndarray型に変換しない)
X = df.iloc[:,:-1]
#目的変数(ndarray型に変換しない)
y = df['MEDV']
#結果格納用のリスト宣言
va_ys = []
y_preds = []
models = []
scores = []
#Kfoldのimport
from sklearn.model_selection import KFold
#交差検証の準備
kf = KFold(n_splits=4, shuffle=True, random_state=71)
#ループで交差検証を行う
for tr_idx, va_idx in kf.split(X):
#訓練データと検証データに分ける
tr_x, va_x = X.iloc[tr_idx], X.iloc[va_idx]
tr_y, va_y = y.iloc[tr_idx], y.iloc[va_idx]
#予測結果の格納
va_ys.append(va_y)
#モデルの学習と格納
model = lgb.LGBMRegressor()
model.fit(tr_x, tr_y)
models.append(model)
#予測結果の格納
y_pred = model.predict(va_x)
y_preds.append(y_pred)
#検証結果の格納
score = mean_squared_error(va_y, y_pred)
scores.append(score)
print(scores)
#最も予測精度が高かった結果を格納
best_y_preds = y_preds[0]
#グラフの描画
fig, ax = plt.subplots()
ax.scatter(va_ys[0], best_y_preds, edgecolors=(0, 0, 0))
ax.plot([y.min(), y.max()], [y.min(), y.max()], 'k--', lw=4)
ax.set_xlabel('Measureed')
ax.set_ylabel('Predicted')
plt.show()
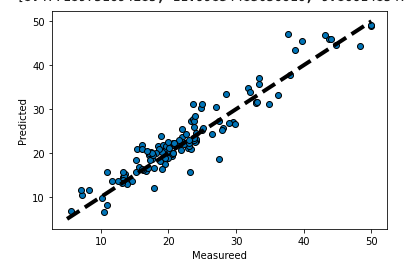
# [8.477189751694285, 11.99834483056616, 9.86614854780343, 22.412387662127898]この例では交差検証を4回繰り返してみました。
そして、評価結果を確認するとループの1番最初に構築したモデルのスコアが最も低いため、それを格納しておき、グラフを描画してみました。モデル精度向上取り組み前に比べて視覚的にもかなりモデルの精度が向上していることを確認できました。
参考資料
この記事はUdemyの以下2つの講座を参考に作成しました。
・【世界で34万人が受講】データサイエンティストを目指すあなたへ〜データサイエンス25時間ブートキャンプ〜
・【キカガク流】人工知能・機械学習 脱ブラックボックス講座 – 初級編 –及び【キカガク流】人工知能・機械学習 脱ブラックボックス講座 – 中級編 –
【世界で34万人が受講】データサイエンティストを目指すあなたへ〜データサイエンス25時間ブートキャンプ〜
当講座は私が1番お勧めできる講座で私も購入済みです。
データサイエンスの定義、統計の考え方、Excelでのデータ分析手法、演習を通じたPythonで機械学習の実装、更にはディープラーニングの実装までとモリモリの内容
重要なセクションごとに演習問題がついているので理解の定着に役立つ
すべて見終えた後に何度も視聴し直すことで確実にAIとデータサイエンスの実践力が身に付く
非常に充実した内容なのですが、一つだけ難点を挙げるとしてたら、26時間にも及ぶ長丁場の講座であるということです。
これを見終えて何度も繰り返し視聴するのは骨が折れますが、マスターすれば大きな武器になることは間違い無いです。
【キカガク流】人工知能・機械学習 脱ブラックボックス講座 – 初級編 –
【キカガク流】人工知能・機械学習 脱ブラックボックス講座 – 中級編 –
株式会社キカガクが作成している【キカガク流】人工知能・機械学習 脱ブラックボックス講座 – 初級編 –及び【キカガク流】人工知能・機械学習 脱ブラックボックス講座 – 中級編 –のシリーズもわかりやすいです。こちらも購入済みです。
初球では単回帰を中級では重回帰の原理を数式を用いて丁寧に解説
Pythonを知らなくても講座の中で学ぶことが可能なので初学者でもOK
それぞれの講座の時間が短いので手軽に学べる
脱ブラックボックスと銘打っているだけあって、機械学習の基礎である、回帰の原理を数式を使いながらステップバイステップで丁寧に説明してくれます。もちろん、解説だけでなくて講義の中で実装もします。
上級はまだ出ていないようなのですが、出たとしたらすぐでも買いたいと思えるシリーズです。
まとめ
ということで、今回はボストンの住宅価格データを使って線形回帰モデルの精度向上に挑戦を挑戦してみました。
記事で書いた通り、精度向上の為にはデータの前処理における外れ値の除去と説明変数の選定、及びモデルのチューニング、モデルの変更、モデルの訓練方法の変更など様々な観点があります。この記事では精度向上のテクニックについて全ては触れられませんでしたが、モデルの精度向上はデータサイエンス領域における永遠の課題と言っても過言ではない深いテーマですので、このブログでも引き続き取り扱っていきたいと思います。
では、今回はここまでとさせていただきます。