【データ分析】MovieLensの映画データを次元圧縮してみる

2022-09-032023-07-12

Pocket

こんにちは、爽です。皆さん、いかがお過ごしでしょうか？

今回は、映画のレビューデータであるMovie Lensを使って次元圧縮をやってみたいと思います。
なお、以前にMovieLensを使ってクラスタリングをやってみたこともあるので、クラスタリングに興味がある方はこちらの記事もご参考ください。

【データ分析】MovieLensを使って映画をクラスタリングで分類してみる

さて、今回の本題の次元圧縮は英語ではDimensionality Reductionと訳すことができ、大量の特徴量をより抽象化することで、少量の特徴量に変換する手法です。用途としてはデータの前処理とデータ可視化の為の補助などです。

なお、今回の記事はnumpy,pandas,matplotlibを理解できている前提で記載しています。
もし上記ライブラリの基本を知りたい方は以下の記事にまとめているので合わせてご参考ください。

・numpy

$【データ分析】numpyの基本を解説！ベクトル・行列・多次元配列の生成と計算$

【データ分析】numpyの基本を解説！ベクトル・行列・多次元配列の生成と計算

・pandas

【データ分析】データを可視化するmatplotlibの基本を解説！

・matplotlib

【データ分析】pandasの基本を解説！Series型とデータフレームの操作

■この記事の対象読者
・データ分析に興味のある方

なお、私はPythonをAnacondaをインストールしてJupyterで実行しています。MacのAnacondaのインストール方法とJupyterの使い方は下記記事にまとめているので良かったらご参考ください。

【基本】Anacondaのインストール方法とJupyterの概要を解説！

それではどうぞ！

次元圧縮とは
データの読み込み
映画データを次元圧縮
次元圧縮結果の解釈
参考資料
まとめ

次元圧縮とは

次元圧縮とは冒頭に記載したように、大量の特徴量をより抽象化することで、少量の特徴量に変換する手法です。これは言い換えると変数同士の相関を確認し、相関が高そうなものに関してはそれらの変数を説明できるような共通の特徴を抽出することと言えるかもしれません。
例えば、塩、醤油、味噌、マヨネーズといった調味料の羅列を見たときに共通している要素は「塩分」が挙げられると思います。もちろん、それら変数の個別の特徴に比べると、共通項として取り出した特徴である「塩分」では全ての変数の特徴を説明しきれませんが、少量の特徴量に変換することはできました。これが次元圧縮です。

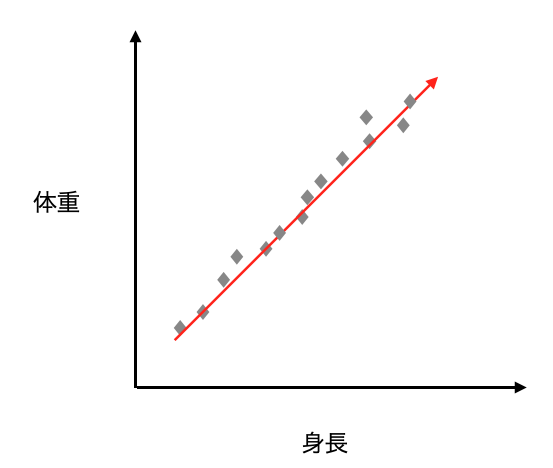
もう1点、よく挙げられる例が身長と体重の例です。
以下の左図のように身長と体重が2次元でプロットされているものを、例えば「ガタイ」という新たな軸を作成することで、身長と体重の特徴を抽出したい上で1次元の特徴量に変換できたと考えるとイメージが湧きやすいかもしれません。
なお、次元圧縮する際は、よく分散の大きい方向で新しい軸を取っていくという表現を使いますが、それはまさに左図の赤矢印のことを指していて、この赤矢印が次元圧縮後の軸となります。

データの読み込み

今回はMovieLensという映画情報とユーザーによるレビュー情報が入っているデータとなります。本来は推薦システムの開発やベンチマークのために作られたデータセットであるようですが、このように分析の題材にも用いられます。今回は読み込んだ映画をいくつかにグルーピングしていくことを目的としていきます。

では早速データを読み込んでいきたいと思います。

import pandas as pd
import numpy as np

import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline

#データセットの読み込み
url = 'http://files.grouplens.org/datasets/movielens/ml-100k/u.item'
#区切り文字の指定とヘッダーの有無と文字コードの指定
df = pd.read_csv(url, sep='|', header=None, encoding='latin-1')
df.head()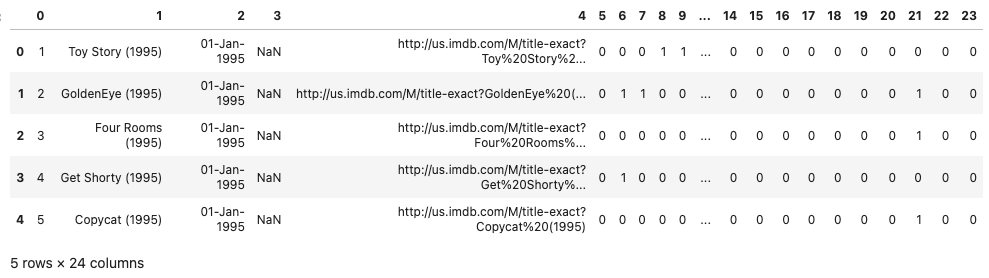

このデータは列名がないので、列名を付与します。

#列情報の追加
#ホームページから取得 http://files.grouplens.org/datasets/movielens/ml-100k-README.txt
col = "id | movie title | release date | video release date | IMDb URL | unknown | Action | Adventure | Animation | Children's | Comedy | Crime | Documentary | Drama | Fantasy | Film-Noir | Horror | Musical | Mystery | Romance | Sci-Fi | Thriller | War | Western"
col_names = col.split(" | ")

#列名を追加
df.columns = col_names
df.head()

各列の意味は以下となります。

movie id：映画のID
movie title：映画のタイトル
release date ：リリース日
video release date：ビデオのリリース日
IMDb URL：データセットの元となるURL（アクセスすると情報が見れる）
6列目以降：映画のジャンル情報（19列分あり、その映画が該当のジャンルの場合は1が振られ、そうでない場合は0となる）

今回は6列目以降の映画のジャンル情報を用いて、19ある映画のジャンルを2次元に圧縮しようと思います。

#ジャンル情報列のみ抽出してこれを学習データとして用いる
X = df.iloc[:, 5:]
X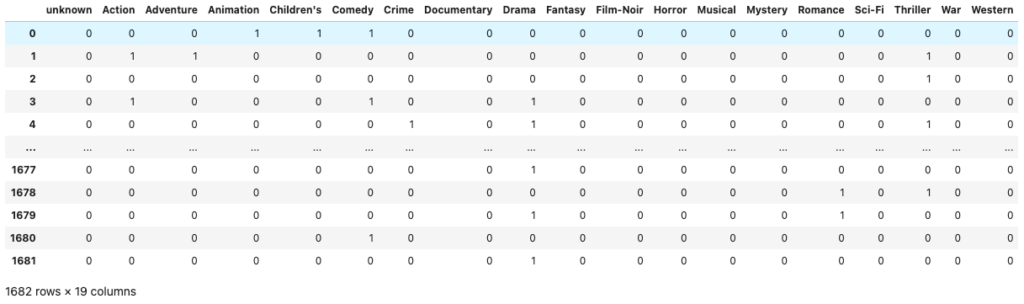

映画データを次元圧縮

ここまででデータを用意できたのでここから次元圧縮をしていきます。今回は次元圧縮のいくつかの手法の中でも代表的な手法である主成分分析（Principle Component Analysis: PCA）をやってみます。主成分分析の概要は以下です。

主成分分析は行列データ（今まで扱っているような表データ）から行列データへの変換処理である
変換された行列データの列は0番目から順に重要度を持っており、この重要度が高い行列データほど、元のデータをよく説明できるものとなっている
- 例えば10列の表データをインプットとした場合、変換後の表データは以下のような情報をもつ
  - 1列目→重要度0.8
  - 2列目→重要度0.1
  - 3列目→重要度0.5
何列目までのデータを使って、元の表データの近似とするかは都度判断が必要

文章だけでは分かりづらいと思うので実際に分析と可視化をしてみます。

#主成分分析のライブラリをimport
from sklearn.decomposition import PCA

#次元圧縮を実行 componentsで何次元に圧縮するかを指定
pca = PCA(n_components=2)
X_pca = pca.fit_transform(X)

はい、たったこれだけで学習ができてしまいました。ではどのような結果になったか確認していきます。

#それぞれの軸の分散説明率を確認
#元データの何割ほど説明ができているかを表す指標
print("分散説明率", pca.explained_variance_ratio_)
print("累積分散説明率", pca.explained_variance_ratio_.sum())

# 分散説明率 [0.2315764  0.17370217]
# 累積分散説明率 0.4052785729098122

分散説明率とは、今回圧縮した2次元の軸それぞれが全体のデータを何割説明できるかを表す指標です。また、累積分散説明率とは上記の分散説明率の合算の値です。
従って、今回作成した軸がどのようなものかは分からないのですが、この2次元の軸を使えば全体の4割ほどを説明できるということが分かります。一方で2次元に圧縮をすることで60%の情報は失われているということは認識した上で結果を解釈していく必要があります。

次元圧縮結果の解釈

さて、では実際にどのような分析結果になったかを見ていきたいと思います。他の分析と同様に次元圧縮も最終的には人手によって結果を解釈していく必要があります。
分析結果を確認するためにはmatplolibで可視化する方法と類似度で測定する方法があります。

可視化

まずはmatplotlibを使って散布図で結果を可視化してみます。まずは映画のタイトルに主成分分析によって求められた特徴量を付与します。

#新たに主成分分析によって求められた2つの特徴量をもつ表データを作成
import copy
pca_df = copy.deepcopy(df[['movie title']])
pca_df['pca1'] = X_pca[:,0]
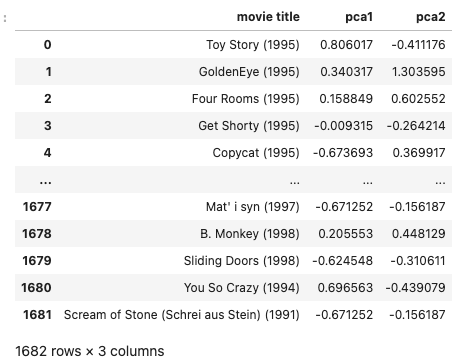
pca_df['pca2'] = X_pca[:,1]
pca_df

次に散布図で可視化します。

pca_df.plot(kind="scatter", x='pca1', y='pca2', figsize=(9, 7), color='pink')

sampled_df = pca_df.sample(50, random_state=0)
plt.scatter(x=sampled_df['pca1'], y=sampled_df['pca2'], color='blue')
for i, row in sampled_df.iterrows():
    x, y, title = row.pca1, row.pca2, row['movie title']
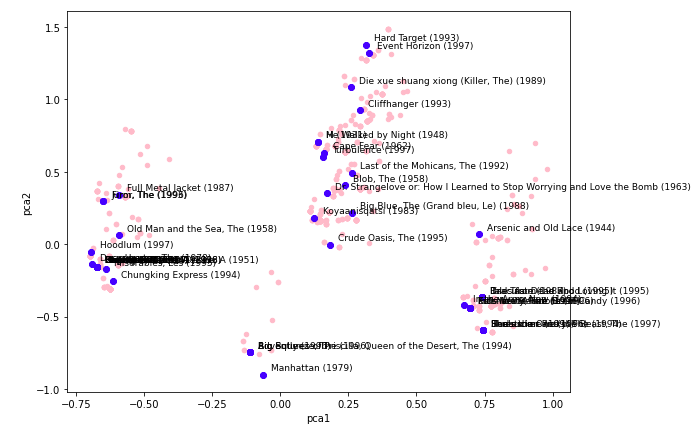
    plt.text(x+.03, y+.03, title, fontsize=9)

新たに生成した2つの軸で映画のプロットができました。
あまり映画に詳しくないので結果の解釈が難しいのですが、pca1とpca2は19のジャンルの共通する何らかの特徴を抽出し、作成された軸であることをmatplotlibの可視化によって確認することが出来ました。

類似度

類似度は機械学習に限らずデータサイエンスでよく用いられる重要な概念の1つで、何らかの尺度に基づいて2つ以上のデータ間の類似性のことを表します。類似度は例えば以下のような場面に使えます。

各クラスタの解釈の例

あるユーザーの購入履歴のある商品の中から、その購入履歴に類似した商品を提案したい（レコメンド）

SNSであるユーザーの特徴に似ているユーザーを推薦したい（レコメンド）

ある書籍の内容を解釈し、その書籍の内容に類似した書籍を分類したい（言語の解釈）

類似度は普段私たちが使っているAmazonやFaceBookでよく見られるようなレコメンドの機能にも導入されていることから、非常な重要な概念であるということが出来ます。また、類似度はレコメンド以外にも例えば文章の構成や用いられている単語からある作家の書籍を分類するというような言語の解釈にも応用することが出来ます。
今回は類似度の中でも比較的に良く用いられるコサイン類似度を用いて映画の類似度を測定していきます。コサイン類似度を求める数式は以下です。

参考：【データサイエンス×ビジネスコミュニケーション】現役データサイエンティストが教える「伝えて動かすデータ分析」

ベクトルの各要素は表データの各列（特徴量）であることから、分子は各特徴量が同じ方向を向いていればいるほど大きくなります。また、この式の計算結果は最終的な指標の値は-1〜+1の範囲に収まり、+1に近いほど類似度は高いと判断ができます。では実際にPythonで実装していきます。

import pandas as pd
import numpy as np

import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline

#コサイン類似度を測定する関数
def cos_sim(v1, v2):
    return np.dot(v1, v2) / (np.linalg.norm(v1) * np.linalg.norm(v2))

#例としてトイストーリーとの類似度を計算
movie_name = 'Toy Story (1995)'
#トイストーリーの主成分分析結果を格納
movie_vector = pca_df[pca_df['movie title'] == movie_name][['pca1', 'pca2']].values[0,:]

#トイストーリーと各映画の類似度を計算
similalities = []
for k, row in pca_df[['pca1', 'pca2']].iterrows():
    similarity = cos_sim(movie_vector, [row['pca1'], row['pca2']])
    similalities.append(similarity)

#データフレームに格納
pca_df['cosine_similarity'] = np.array(similalities)

#類似度の高い順に並び替え
pca_df.sort_values(by='cosine_similarity', ascending=False).head()

分析結果を見ると同じディズニーシリーズである、アラジンの映画が類似度が高いと出ていることから、コサイン類似度の計算は成功していそうです。他の映画でも試してみるのも面白いと思います。
このようにコサイン類似度を適用することでも、分析結果を解釈することができました。

参考資料

この記事はUdemyの【データサイエンス×ビジネスコミュニケーション】現役データサイエンティストが教える「伝えて動かすデータ分析」という講座を参考にさせていただき、作成しました。

【データサイエンス×ビジネスコミュニケーション】現役データサイエンティストが教える「伝えて動かすデータ分析」

当講座のおすすめポイントを以下にまとめておきます。

当講座のおすすめポイント

Pythonを知らなくても講座の中で学ぶことが可能なので初学者でもOK

データサイエンスの手法だけでなく、それをどのようにビジネスに活かすかまで学べる

この講座の最大の特徴は、データサイエンスを実務でどのように活かすかまで言及されている点です。
他の講座だとデー分析の手法や機械学習の実装方法だけ伝えるものもあるのですが、この講座はデータサイエンスの習得を目的とせず、その先を見据えた講義になっているので、実務での使用イメージが湧きやすいです。

なお、Udemyについては以下の記事でまとめていますのでご参考ください。

現役コンサルタントがUdemyの特徴とおすすめ講座を厳選して紹介

まとめ

ということで、今回は映画のレビューデータであるMovie Lensを使って次元圧縮をやってみました。
今回の例だと次元圧縮の有用性はあまり感じられないかもしれないのですが、例えば大量にある特徴量を次元圧縮で新たな特徴を作成するといったようなデータの前処理の部分で威力を発揮するかもしれません。私も次元圧縮について学んでこのブログで有用性を感じられるような例を紹介できればと思っています。
では、今回はここまでとさせていただきます。

Python,キャリア